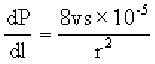
TRANSLOCATION OF NUTRIENTS IN THE PHLOEM: POISEUILLE'S EQUATION

Introduction: Plant biologists spent many decades trying to understand the mechanisms behind transport of nutrients through seive tubes in the phloem. Proponents of mass transport believed the gradient of solute concentration along seive tubes would create a gradient of turgor pressure. The pressure gradient could be quite small (0.020 Mpa per meter) but still be enough to drive the flow of nutrients (see Dixon's Paradox). However, the idea of mass transport seemed too simplistic for many plants whose cell-to-cell pressure gradient or speed of transfer did not match that predicted by Dixon's equation.

Importance: The pressure gradient along the length of a plant is related to the width of the seive tubes as well as the viscosity of the solution. We can use an equation to calculate expected pressure gradients and compare these results with those of mass transport.

Question: How is the pressure gradient affected by the size of sieve tubes? How does this cast doubt on the idea of mass transport?

Variables:

Methods:

The Poiseuille equation cast doubts on the feasability of mass transport. This equation assumes that the pressure gradient (dP/dl) created by differences in carbon concentration between phloem cells depends on the width of those cells and the viscosity of the solution. A useful form of this equation is:

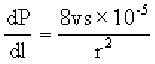
 where v is the viscosity of the solution (around 0.015 poise), s is the speed of transfer (cm/s), and r is the radius of the tube (cm).

If we graph dP/dl as a function of r, we can assess how the pressure gradient required to maintain mass transfer varies with size of the seive tubes.

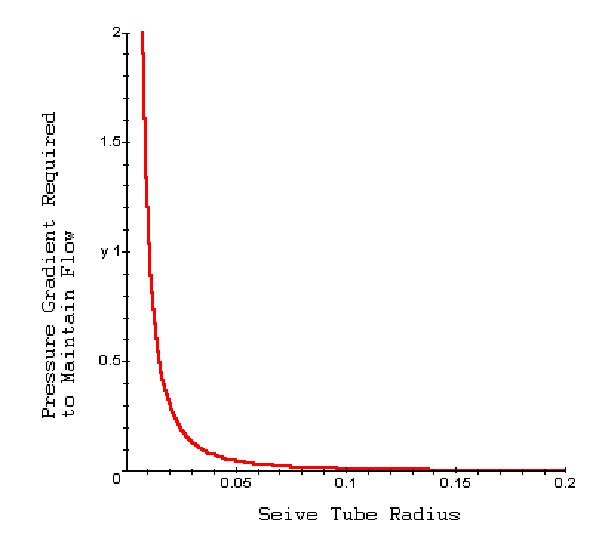
Interpretation: For plants with wide seive tubes (25 to 50 μm), only small differences in internal pressure are needed to drive the flow. This favors the idea of mass transport which assumes small differences in carbon concentration can drive the transfer of nutrients. However, a great majority of plants have very small seive tubes (5 μm) and seive pores (0.7 μm) and require very large pressure gradients (from 0.04 to 4 MPa per meter) for flow to occur at a speed of around 100 cm/hour. This does not match the idea of mass transfer.

If the cell to cell pressure gradient in plants is not large enough to drive flow, than what is driving nutrient transport? Milburn (1974) showed the pressure gradient appeared unrelated to the gradient of solute concentration as proponents of mass transport believed. The pressure near leaf sources fell dramatically from 1.6 MPa to 1.2 MPa right below the leaves, remained constant down the length of the plant, and again dropped dramatically to 0.6 MPa just above the roots. Consequently, the pressure gradient from source to sink would be sufficient to drive flow, but not the negligible pressure gradient inbetween.

Conclusions: Proponents of mass transport generally tested their theory with plants with wide sieve tubes. The concentration gradient between cells was quite small, but enough to drive the flow of nutrients. However, most plants have much smaller sieve tubes and would require much larger pressure gradients between cells in order to drive flow. Poiseuille's equation quantified how the pressure gradient is related to seive tube size and raised questions about the feasibility of mass transfer.

Sources: M. J. Canny. 1984. Translocation of nutrients and hormones, p. 277-296 in Advanced Plant Physiology. M. B. Wilkins, ed. Pitman Publishing Limited, Marshfield, MA

J. A. Milburn. 1974. Phloem transport in Ricinus. Concentration gradients between source and sink. Planta 117:303-319

Copyright 1999 M. Beals, L. Gross, S. Harrell